I alla mätsystem – från trådlös kommunikation till digital fotografering – är signal-brusförhållandet (SNR) ett grundläggande måttstock för kvalitet. Oavsett om du analyserar teleskopbilder, förbättrar mikrofoninspelningar eller felsöker en trådlös länk, visar SNR hur mycket användbar information som sticker ut från oönskat bakgrundsbrus.
Men att beräkna signal-brusförhållandet korrekt är inte alltid enkelt. Beroende på systemet kan ytterligare faktorer som mörkström, läsbrus eller pixelbinning behöva beaktas. Den här guiden guidar dig genom teorin, kärnformlerna, vanliga misstag, tillämpningar och praktiska sätt att förbättra signal-bruset, vilket säkerställer att du kan tillämpa det korrekt i en mängd olika sammanhang.
Vad är signal-brusförhållande (SNR)?
I grund och botten mäter signal-brusförhållandet förhållandet mellan styrkan hos en önskad signal och bakgrundsbruset som skymmer den.
● Signal = den meningsfulla informationen (t.ex. en röst i ett samtal, en stjärna i en teleskopbild).
● Brus = slumpmässiga, oönskade fluktuationer som förvränger eller döljer signalen (t.ex. statisk støj, sensorbrus, elektrisk störning).
Matematiskt definieras signal-brusförhållandet (SNR) som:
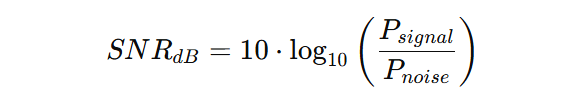
Eftersom dessa förhållanden kan variera över många storleksordningar uttrycks signal-brusförhållandet (SNR) vanligtvis i decibel (dB):
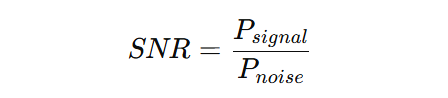
● Högt signal-brusförhållande (t.ex. 40 dB): signalen dominerar, vilket resulterar i tydlig och tillförlitlig information.
● Lågt signal-brusförhållande (t.ex. 5 dB): brus överskuggar signalen, vilket gör tolkningen svår.
Hur man beräknar signal-/brusförhållande (SNR)
Beräkning av signal-brusförhållandet kan utföras med olika precisionsnivåer beroende på vilka bruskällor som ingår. I detta avsnitt kommer två former att introduceras: en som tar hänsyn till mörkström och en som antar att den kan försummas.
Obs: Att addera oberoende brusvärden kräver att de adderas i kvadratur. Varje bruskälla kvadreras, summeras och kvadratroten av totalen tas.
Signal-brusförhållande med mörkström
Följande är ekvationen som ska användas i situationer där mörkströmsbruset är tillräckligt stort för att kräva inkludering:
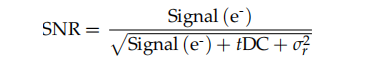
Här är definitionen av termerna:
Signal (e-): Detta är den aktuella signalen i fotoelektroner, med mörkströmssignalen subtraherad
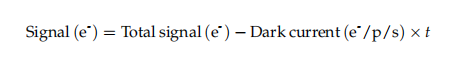
Den totala signalen (e-) kommer att vara fotoelektronantalet i den aktuella pixeln – absolut inte pixelvärdet i enheter av grånivåer. Den andra förekomsten av signalen (e-), längst ner i ekvationen, är fotonskottbruset.
Mörkström (DC):Mörkerströmsvärdet för den pixeln.
t: Exponeringstid i sekunder
σr:Läs brus i kameraläge.
Signal-brusförhållande för försumbar mörkström
I fall av korta (< 1 sekund) exponeringstider, plus kylda, högpresterande kameror, kommer mörkströmsbruset i allmänhet att ligga långt under läsbruset och säkert försummas.

Där termerna återigen är som definierats ovan, med undantaget att mörkerströmssignalen inte behöver beräknas och subtraheras från signalen eftersom den borde vara lika med noll.
Begränsningar med dessa formler och saknade termer
Formlerna mittemot ger endast korrekta svar för CCD ochCMOS-kamerorEMCCD och intensifierade enheter introducerar ytterligare bruskällor, så dessa ekvationer kan inte användas. För en mer komplett signal-brusförhållandeekvation som tar hänsyn till dessa och andra bidrag.
En annan brusterm som vanligtvis ingår (eller brukade användas) i SNR-ekvationer är fotoresponsnonuniformitet (PRNU), ibland även kallad "fast mönsterbrus" (FPN). Detta representerar ojämnheter i förstärkning och signalrespons över sensorn, vilket kan bli dominerande vid höga signaler om det är tillräckligt stort, vilket minskar SNR.
Medan tidiga kameror hade tillräckligt betydande PRNU för att kräva dess inkludering, var de flesta modernavetenskapliga kamerorhar tillräckligt låg PRNU för att bidra långt under fotonbruset, särskilt efter att inbyggda korrigeringar har tillämpats. Det försummas därför numera vanligtvis i SNR-beräkningar. PRNU är dock fortfarande viktigt för vissa kameror och tillämpningar och ingår i den mer avancerade SNR-ekvationen för fullständighetens skull. Detta innebär att de angivna ekvationerna är användbara för de flesta CCD/CMOS-system men bör inte behandlas som universellt tillämpliga.
Typer av brus i SNR-beräkningar
Att beräkna signal-brusförhållandet (SNR) handlar inte bara om att jämföra en signal med ett enda brusvärde. I praktiken bidrar flera oberoende bruskällor, och det är viktigt att förstå dem.
Skottbuller
● Ursprung: statistisk ankomst av fotoner eller elektroner.
● Skalar med kvadratroten av signalen.
● Dominerande inom fotonbegränsad avbildning (astronomi, fluorescensmikroskopi).
Termiskt brus
● Det kallas även Johnson-Nyquist-brus och produceras av elektronrörelse i motstånd.
● Ökar med temperatur och bandbredd.
● Viktigt inom elektronik och trådlös kommunikation.
Mörkt strömbrus
● Slumpmässig variation i mörkerström inom sensorer.
● Mer betydande vid långa exponeringar eller varma detektorer.
● Minskad genom kylning av sensorn.
Läs brus
● Brus från förstärkare och analog-till-digital-omvandling.
● Fast per avläsning, så avgörande vid låg signal.
Kvantiseringsbrus
● Introducerades genom digitalisering (avrundning till diskreta nivåer).
● Viktigt i system med lågt bitdjup (t.ex. 8-bitars ljud).
Miljö-/systembuller
● EMI, överhörning, rippel i strömförsörjningen.
● Kan dominera om skärmningen/jordningen är dålig.
Att förstå vilken av dessa som är dominerande hjälper till att välja rätt formel och metod för att mildra effekterna.
Vanliga misstag vid beräkning av signal-/støy-/brusförhållande (SNR)
Det är lätt att stöta på många "genvägsmetoder" för att uppskatta signal-brusförhållandet vid avbildning. Dessa tenderar att vara antingen mindre komplexa än ekvationerna mittemot, möjliggöra enklare härledning från själva bilden snarare än att kräva kunskap om kameraparametrar som läsbrus, eller båda. Tyvärr är det troligt att var och en av dessa metoder är felaktiga och kommer att leda till snedvridna och ohjälpsamma resultat. Det rekommenderas starkt att ekvationerna mittemot (eller den avancerade versionen) används i alla fall.
Några av de vanligaste falska genvägarna inkluderar:
1. Jämförelse av signalintensitet kontra bakgrundsintensitet, i grånivåer. Denna metod försöker bedöma kamerakänslighet, signalstyrka eller signal-brusförhållande genom att jämföra en toppintensitet med en bakgrundsintensitet. Denna metod är djupt bristfällig eftersom påverkan av kamerans offset godtyckligt kan ställa in bakgrundsintensiteten, förstärkning kan godtyckligt ställa in signalintensiteten, och inget bidrag från brus vare sig i signal eller bakgrund beaktas.
2. Att dividera signaltoppar med standardavvikelsen för ett område med bakgrundspixlar. Eller att jämföra toppvärden med det visuella bruset i bakgrunden som avslöjas av en linjeprofil. Om man antar att offseten subtraheras korrekt från värdena före division, är den största faran med denna metod närvaron av bakgrundsljus. Allt bakgrundsljus kommer vanligtvis att dominera bruset i bakgrundspixlarna. Dessutom beaktas inte bruset i den aktuella signalen, såsom skottbrus, alls.
3. Medelsignal i intressanta pixlar kontra standardavvikelse för pixelvärden: Att jämföra eller observera hur mycket en toppsignal förändras över angränsande pixlar eller efterföljande bildrutor är närmare att vara korrekt än andra genvägsmetoder, men det är osannolikt att man undviker andra faktorer som förvränger värden, såsom en förändring i signalen som inte härrör från brus. Denna metod kan också vara felaktig på grund av lågt pixelantal i jämförelsen. Subtraktion av offsetvärdet får inte heller glömmas bort.
4. Beräkning av signal-brus (SNR) utan att konvertera till intensitetsenheter för fotoelektroner, eller utan att ta bort offseten: Eftersom fotonbrus vanligtvis är den största bruskällan och förlitar sig på kunskap om kamerans offset och förstärkning för mätning, är det inte möjligt att undvika beräkning tillbaka till fotoelektroner för SNR-beräkningar.
5. Bedömning av signal-brusförhållandet med ögat: Även om det under vissa omständigheter kan vara användbart att bedöma eller jämföra signal-brusförhållandet med ögat, finns det också oväntade fallgropar. Att bedöma signal-brusförhållandet i pixlar med högt värde kan vara svårare än i pixlar med lägre värde eller bakgrundspixlar. Mer subtila effekter kan också spela en roll: Till exempel kan olika datorskärmar rendera bilder med mycket olika kontrast. Dessutom kan visning av bilder med olika zoomnivåer i programvara avsevärt påverka det visuella utseendet på brus. Detta är särskilt problematiskt om man försöker jämföra kameror med olika pixelstorlekar i objektutrymmet. Slutligen kan närvaron av bakgrundsljus omöjliggöra alla försök att bedöma signal-brusförhållandet visuellt.
Tillämpningar av signal-/signalförhållande (SNR)
SNR är ett universellt mått med brett användningsområde:
● Ljud- och musikinspelning: Bestämmer inspelningarnas klarhet, dynamiskt omfång och återgivning.
● Trådlös kommunikation: SNR relaterar direkt till bitfelsfrekvenser (BER) och dataflöde.
● Vetenskaplig avbildning: Inom astronomi kräver det högt signal-brusförhållande (SNR) för att upptäcka svaga stjärnor mot bakgrundsljus.
● Medicinsk utrustning: EKG-, MR- och CT-skanningar använder högt signal-/brusförhållande (SNR) för att skilja signaler från fysiologiskt brus.
● Kameror och fotografering: Både konsumentkameror och vetenskapliga CMOS-sensorer använder signal-brusförhållande (SNR) för att jämföra prestanda i svagt ljus.
Förbättra signal-/brusförhållandet
Eftersom signal-/brusförhållande (SNR) är ett så viktigt mått läggs betydande ansträngningar ner på att förbättra det. Strategierna inkluderar:
Hårdvarumetoder
● Använd bättre sensorer med lägre mörkerström.
● Använd skärmning och jordning för att minska EMI.
● Kyldetektorer för att dämpa termiskt brus.
Programvarumetoder
● Använd digitala filter för att ta bort oönskade frekvenser.
● Använd medelvärdesberäkning över flera bildrutor.
● Använd brusreduceringsalgoritmer i bild- eller ljudbehandling.
Pixelbinning och dess effekt på signal-brusförhållande
Effekten av binning på signal-brusförhållandet beror på kamerateknik och sensorbeteende, eftersom brusprestandan hos binnade och icke-binnade kameror kan variera avsevärt.
CCD-kameror kan summera intilliggande pixlars laddning "på chipet". Avläsningsbruset uppstår bara en gång, även om mörkströmssignalen från varje pixel också summeras.
De flesta CMOS-kameror utför off-chip-binning, vilket innebär att värden först mäts (och läsbrus introduceras) och sedan summeras digitalt. Läsbruset för sådana summeringar ökar genom multiplikation med kvadratroten ur antalet summerade pixlar, dvs. med en faktor 2 för 2x2-binning.
Eftersom sensorers brusbeteende kan vara komplicerat, är det för kvantitativa tillämpningar lämpligt att mäta kamerans offset, förstärkning och avläsningsbrus i binned-läge och använda dessa värden för signal-brusförhållandet.
Slutsats
Signal-brusförhållandet (SNR) är ett av de viktigaste måtten inom vetenskap, teknik och teknologi. Från att definiera tydlighet i telefonsamtal till att möjliggöra detektering av avlägsna galaxer, ligger SNR till grund för kvaliteten på mät- och kommunikationssystem. Att behärska SNR handlar inte bara om att memorera formler – det handlar om att förstå antaganden, begränsningar och verkliga avvägningar. Ur detta perspektiv kan ingenjörer och forskare göra mer tillförlitliga mätningar och designa system som utvinner meningsfulla insikter även i bullriga förhållanden.
Vill du veta mer? Ta en titt på relaterade artiklar:
Tucsen Photonics Co., Ltd. Med ensamrätt. Vänligen ange källan vid citering:www.tucsen.com

 25/09/11
25/09/11